Collin Moshman
Poker Expert
Silver Level
If you have any specific questions about one of the examples, I'd be happy to answer.
As another off-the-cuff example:
Suppose we hold: 8s6h.
The flop is: Kh 4d 5s
The pot is $100 and our opponent moves all-in for $100.
In this case, our pot odds are $200 : $100 (total pot is $200 and it costs $100) to call. This simplifies to 2:1.
We decide whether to call based on the likelihood we hit our draw -- the more likely we hit, and the better the odds, the more favorable calling is. Here we can use the odds chart from this article to see that we're not getting the odds we need.
We want odds of 5:1 with an inside straight draw at the flop, but we're only getting 2:1 so we have to fold.
H
hanio75
Enthusiast
Silver Level
Hello Collin! Thank you for your help. But how did you determine that we need 5:1 odds?
vinnie
Legend
Bronze Level
He linked to an article which has a table of odds and draws. A gutshot draw with two cards to come is 5-1.
There are ways to do this at the table, but you get an idea pretty quickly. The fewer outs you have, the larger the pot needs to be for it to be worth it. Our odds for this actual hand are even better than 5-1, but still not high enough to call when getting 2-1. We have some backdoor draws here (2,3,6,8) which help our hand. Usually, you can ignore those. Things would have to be really close for those backdoor draws to change a fold into a call.
There are ways to do this at the table, but you get an idea pretty quickly. The fewer outs you have, the larger the pot needs to be for it to be worth it. Our odds for this actual hand are even better than 5-1, but still not high enough to call when getting 2-1. We have some backdoor draws here (2,3,6,8) which help our hand. Usually, you can ignore those. Things would have to be really close for those backdoor draws to change a fold into a call.
Katie Dozier
Poker Expert
Silver Level
iv_horsemen
Enthusiast
Silver Level
This is a totally new concept for me. Guess I'm a weak player who's more worried about if I got the best had and need to change my thought process altogether. Think I'll watch that video again and read through the odds for dummies section and reserve my questions for after.
iv_horsemen
iv_horsemen
H
hanio75
Enthusiast
Silver Level
Hi Vinnie I had not noticed. Thanks for the guidance, I'll see if I can understand. Thank you very much.
H
hanio75
Enthusiast
Silver Level
Hi Collin, I was lost, but mow I'm reading the article and seeking to understand. Now I just need to try to check these concepts when I was playing at a table . Thank you.
Collin Moshman
Poker Expert
Silver Level
Yes exactly, thanks for posting. For me internally, I often go from outs -> percentages -> odds which is probably not the most efficient way of thinking
But like you say, we can at least have a good idea quickly, or just keep access to charts like this when playing online.
It's just a different way of thinking that will often be important based on the odds. If you're getting great odds, you can have a hand that is likely beat but still be correct to call. Watch again and post with any questions. You'll get good at it fast!
Hi Collin, I was lost, but mow I'm reading the article and seeking to understand. Now I just need to try to check these concepts when I was playing at a table . Thank you.
That's great Hanio, glad to hear!
lollipopas
Enthusiast
Silver Level
Hi, I'm trying to think through this with a hand I played.
Here's a link to the replayer (it's a bit tricky to find the hand anymore for the forum code, but I have the replayer link I made earlier. The text description can be found in "details" button on the top right of the replayer)
https://www.cardschat.com/replayer/224Eb9wDO
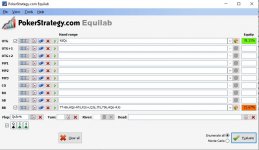
So I calculate equity in Equilab - I put my cards in, and the range for calling UTG open raise for BB. It gives me 44% equity.
Turns out both me and BB were a little bit loose in our ranges.
After the flop, it gives me 78.33% equity.
BB shoves into me (is it donk-shoving then?)
Pot is 1135, BB shoves 1740. Now pot 2875 and it costs me 1740 to call, so odds are 1.65 to 1, or I need to be correct 37% of the time (1/ (1.65 + 1))
So if I compare it to my 78.33% equity (or 0.28 to 1 odds?), calling here is correct?
My thinking: I have top pair strong kicker. Shoving looks very suspicious (as it turns out, flush draw. Otherwise might be someone who got extra excited about having some sort of queen (they would likely just cbet QA)? or just complete bluff)
Would I think in a similar way for villain's decision?
So after flop against my presumed range V has 39.9% equity. So shoving 1740 to win 1135 (in case I fold) has pot odds of 0.65 to 1, so 60% is how often I need to fold for it to be profitable (and that's only if when I call I always win, right? they still have outs if I call as we see in how it played out). And then for when I call, it's the same pot odds as they were for my calculation, so he needs to be correct 37% of the time, and he has 39.9% equity, so it's a good decision to shove.
Here's a link to the replayer (it's a bit tricky to find the hand anymore for the forum code, but I have the replayer link I made earlier. The text description can be found in "details" button on the top right of the replayer)
https://www.cardschat.com/replayer/224Eb9wDO
So I calculate equity in Equilab - I put my cards in, and the range for calling UTG open raise for BB. It gives me 44% equity.
Turns out both me and BB were a little bit loose in our ranges.
After the flop, it gives me 78.33% equity.
BB shoves into me (is it donk-shoving then?)
Pot is 1135, BB shoves 1740. Now pot 2875 and it costs me 1740 to call, so odds are 1.65 to 1, or I need to be correct 37% of the time (1/ (1.65 + 1))
So if I compare it to my 78.33% equity (or 0.28 to 1 odds?), calling here is correct?
My thinking: I have top pair strong kicker. Shoving looks very suspicious (as it turns out, flush draw. Otherwise might be someone who got extra excited about having some sort of queen (they would likely just cbet QA)? or just complete bluff)
Would I think in a similar way for villain's decision?
So after flop against my presumed range V has 39.9% equity. So shoving 1740 to win 1135 (in case I fold) has pot odds of 0.65 to 1, so 60% is how often I need to fold for it to be profitable (and that's only if when I call I always win, right? they still have outs if I call as we see in how it played out). And then for when I call, it's the same pot odds as they were for my calculation, so he needs to be correct 37% of the time, and he has 39.9% equity, so it's a good decision to shove.
Attachments
vinnie
Legend
Bronze Level
There is a lot to break down here.
First off, I am not sure what you mean by the preflop equity. I don't think you were too loose. But let's talk about the flop. That is really where the range discussion comes in. But, you should see that the ranges really don't play a huge role. In both cases, the hands here play themselves.
We don't compare the BB's equity from a shove against your range for raising UTG preflop. We compare it with the range you will call his shove with. With this specific hand, we can assume we are never good when called but that we will win if we hit the flush. This is normally true, except for times you have QQ or AcQc here.
That means we expect to have 35% equity when called. We need 37.7% to break even. In general when the SPR is near one, we are getting just about the right price to never fold a flush draw heads up on the flop. Here we expect to lose about 125 chips when UTG calls. But, we also can expect a fair amount of folds. We are risking 125 chips to win 1135, which means we only need a fold about 10% of the time to break even here. I expect more than 10% of UTG's range will fold here. So shoving will probably show a profit.
Your decision is a lot easier. Most of the hands that you worry about on this flop would raise preflop. AA, KK, AQ, QQ for example. Without a raise preflop, you can assume those hands are very unlikely. You are very rarely behind here. I expect a worse queen or a flush draw 70%+ of the time here. There might be some smaller pairs and other stuff in the other 30% but most of that you're crushing also You easily have the right amount of equity to call against that range. You aren't looking at how you do against his preflop range, just the range of hands that are likely to shove this flop that are left from his preflop range. In short, I snap call with these stacks and as played.
BB gets there on the turn. Nice hand BB. Shake it off and keep playing right.
Katie Dozier
Poker Expert
Silver Level
Excellent job on breaking down what the math looks like in this particular situation—well done and it looks good to me [emoji4]
Katie Dozier
Poker Expert
Silver Level
This is an excellent reply here from Vinnie with great adjustments to narrow down those hand ranges [emoji4]
lollipopas
Enthusiast
Silver Level
Thanks for detailed answer. I followed most of it and understood it, but I'm a bit confused about the above part. So you're talking about the shoving situation from the point of view of BB here?
But where is "expect to lost about 125 chips when UTG calls"? Where is 125 coming from?
vinnie
Legend
Bronze Level
You are right. I was talking from the perspective of the BB there. Sorry, I wasn't super clear about it.
As the BB, assume you know nothing about what hand the UTG player has. If you shove and they have nothing, they will fold. So, we don't need to worry about what hands they will fold. But, if they do call, we can be pretty sure that pairing the Jack or the 9 will not be enough to win. It could be, but we want to keep these thoughts simple at the table. We assume that if we hit the flush, we will win. This isn't always true (KcQc or AcQc for example have us in horrible shape), but again, we try and keep things simple at the table. We could try and compile a whole range here, and then find our equity against it, but at the table we need to try and keep things approachable. We assume the flush will win and a pair won't. So, we only need to think about our odds of hitting the flush draw.
We have 9 outs, twice, which means we have about 36% equity. I used 35%, which is close enough. If we shove and get called, we can assume that we have about 35% equity in the 4,615 chip pot. That mean we get 1,615 chips back, but it cost us 1,740 chips to get here, so we lost about 125 chips when we got called. That's what I meant. Slightly different assumptions about our equity will change this number. We really only have 32.22% equity in this specific circumstance, so it actually costs us about 253 chips when we get called. But, against a more balanced range [66+,Qx] we have 36.15% equity and getting called would cost 72 chips. These are all estimates, and we can't be sure of things at the table. So we make a guess and get a number. 125 chips turns out to be a really decent estimate.
Now the full fold-equity calculation is: fold% * PotSize + (100% - fold%) * {equity% * (PotSize + 2 * BetSize) - BetSize}
This is a mess and is really bulky. We don't want to be doing this at the table. But, we already know the value of "{equity% * (PotSize + 2 * BetSize) - BetSize}" to be -125 chips. We figured that out in the above. So instead of thinking about betting 1740 with 35% equity, we can just pretend we're betting 125 with 0% equity. It makes the whole thing simpler and it works because that bet costs us 125 chips when it is called.
So, we can just say that we're risking 125 to win the 1,135 that is out there. If we do the exact math, we need like 12.38% fold equity. But, we don't need to be that specific. Actually, we shouldn't even pretend to be that specific with the assumptions we have made. So, if he folds 1 time in 10 or 1 time in 8, we will break even. He's probably folding a lot more than that.
lollipopas
Enthusiast
Silver Level
Thanks, it makes more sense about the mystical 125 chips.
A bit of a tangent here - just wanted to ask if I'm right with applying a concept of blockers here as well.
So since I have a Qc, am I right to think that it makes it less likely that BB is on a flush draw? (So when I'm trying to think about his range when he shoves, and say put him on, like you said, most of the time a weak queen or a flush draw, with some possibility of smaller pair, would it then make me think that since I have a club in my hand, then BB is more likely to have a weak queen or a small pair and not a flush draw, because my Qc is a blocker?)
vinnie
Legend
Bronze Level
When considering blockers, saying a type of hand is more likely than another is relative. In this case, the fact that you know where two Queens are (one in your hand and one on board) is probably more significant than that you know where three clubs are (one in your hand and two on board). I'm stating that before constructing a range and running some numbers, but I'm going to do that. So, my gut feeling is that holding the Qc makes it more likely this is a flush draw.
I'll check my gut feeling by constructing a range and seeing what happens. Let's construct an example range.
[ TT - 77 {assume he shoves pairs larger or smaller than this preflop}
ATs - A2s, KQs - K3s, QJs - Q6s, JTs - J7s, T9s - T7s, 98s - 96s, 78s -76s,
AJo - A6o, KQo - K9o, QJo - Q9o, JTo - J9o, T9o, 98o, 87o]
I feel like this is a reasonable calling range. I'd have shoved some of these hands with the stack sizes, and I would fold a couple of these. But it seems reasonable to me. You can always play with ranges that you feel are more appropriate.
This original range includes seven Qxs hands and four Qxo hands. That's 76 combinations of Qx. There are 37 suited cc hands, for 37 combinations (we only care about the ones with clubs on this flop).
The flop knocks out a bunch of Qx hands, because it has a queen on it. We drop to 57 combinations (anything with the Qs is no longer possible). The flop only removes 4 flush combinations, so down to 33 possible flushes. And 24 combinations of pairs (77-TT). That's 50% Qx, 29% flushes, and 21% pairs. Knowing our hand contains a KdQc removes another 21 combinations of queens bringing us down to 36. Holding the Qc brings us down to 26 combinations of flushes. The end result is 42% Qx, 30% flushes, and 28% pairs.
From 57 to 36 is a 37% drop. From 33 to 26 is a 21% drop. So holding the Qc actually removed a higher percentage of Qx hands than it removes flushes. The amount of smaller pairs didn't change at 24 combinations. The overall effect is that flushes are slightly more likely than if we didn't know anything about our hand. The biggest change was the Qx, because we know where half the queens in the deck are.
Yes, holding a club does reduce the ways your opponent holds a flush. But, if your holding is strong enough to call, the rank of your cards is usually going to remove more pair combinations than having one of the suit removes flush combinations. The nice thing about having that card is that when you are against a flush you're making it harder for your opponent to hit.
I'll check my gut feeling by constructing a range and seeing what happens. Let's construct an example range.
[ TT - 77 {assume he shoves pairs larger or smaller than this preflop}
ATs - A2s, KQs - K3s, QJs - Q6s, JTs - J7s, T9s - T7s, 98s - 96s, 78s -76s,
AJo - A6o, KQo - K9o, QJo - Q9o, JTo - J9o, T9o, 98o, 87o]
I feel like this is a reasonable calling range. I'd have shoved some of these hands with the stack sizes, and I would fold a couple of these. But it seems reasonable to me. You can always play with ranges that you feel are more appropriate.
This original range includes seven Qxs hands and four Qxo hands. That's 76 combinations of Qx. There are 37 suited cc hands, for 37 combinations (we only care about the ones with clubs on this flop).
The flop knocks out a bunch of Qx hands, because it has a queen on it. We drop to 57 combinations (anything with the Qs is no longer possible). The flop only removes 4 flush combinations, so down to 33 possible flushes. And 24 combinations of pairs (77-TT). That's 50% Qx, 29% flushes, and 21% pairs. Knowing our hand contains a KdQc removes another 21 combinations of queens bringing us down to 36. Holding the Qc brings us down to 26 combinations of flushes. The end result is 42% Qx, 30% flushes, and 28% pairs.
From 57 to 36 is a 37% drop. From 33 to 26 is a 21% drop. So holding the Qc actually removed a higher percentage of Qx hands than it removes flushes. The amount of smaller pairs didn't change at 24 combinations. The overall effect is that flushes are slightly more likely than if we didn't know anything about our hand. The biggest change was the Qx, because we know where half the queens in the deck are.
Yes, holding a club does reduce the ways your opponent holds a flush. But, if your holding is strong enough to call, the rank of your cards is usually going to remove more pair combinations than having one of the suit removes flush combinations. The nice thing about having that card is that when you are against a flush you're making it harder for your opponent to hit.
Last edited:
lollipopas
Enthusiast
Silver Level
Thanks for explaining. Very interesting about overall effect making flushes slightly more likely, but also making it harder for the opponent to hit a flush.
vinnie
Legend
Bronze Level
Thanks, but blockers are a very complicated subject and I was just trying to think through this one situation. My gut feeling was that, considering the range we thought would shove, the Queen removed more top-pair combinations than flush draws. With the ranges I assumed, it was slightly true.
I am still fairly new with the concept of blockers. And, I'm definitely not the best resource to go to. There are times where holding one of the flush cards will remove a significant amount of the flush-draws our opponent will have in his range. I think this was a decent walk-through of this situation, although I wouldn't be too surprised if someone came around and pointed out errors in it.
Jim Rivas
Visionary
Bronze Level
I know how to calculate POT ODDS and ODDS using OUTS, but implicit ODDS and expected value, no idea how they are done.